36 years on the
Pattern Recognition Front

Theo Pavlidis

Lecture given at ICPR’2000 in Barcelona, Spain
on the occasion of receiving the K.S. Fu prize.

Summary

The talk consists of four parts: How I became interested in Pattern Recognition (and a bit of Personal History). - The Early Years of Pattern recognition (Late 60’s and 70’s). - Pattern recognition in the Present (the last 20 years). - Suggestions for the Future and Prospects. The word "front" in the title should be read in the same way as in the phrase "Western Front."

1. How I became interested in Pattern Recognition

It is appropriate to start the lecture by explaining how I became interested in Pattern Recognition which in turn requires a bit of personal history. In the Fall of 1961 I started graduate studies at the University of California at Berkeley. Before arriving there I had spent a few years working in a power plant in Greece where I had been fascinated by control mechanisms and I was looking forward to pursuing a Ph.D. in Control Theory.

I was in for a major disappointment. Control Theory in the academia had become a purely mathematical field, staying away from any problem that had any trace of applications or practical usefulness. In addition, it relied on obsolete mathematics from the early part of the 19^th century. Being at Berkeley, I came  across Hermann Hesse's books that were at the height of their popularity there. (There was even a bar named Steppenwolf.) When I read Magister Ludi I recognized immediately, the modern version of the glass bead game (the Glassperlenspiel): it was Academic Control Theory as practiced at Berkeley and other top U.S. Universities. The most attractive part of engineering, the creative interaction between theory and practice, had been discarded.

I was thinking of dropping out (an event that would have had far more serious consequences for a foreign student than a domestic one). After all, who was I to challenge the wisdom of all these famous American professors. Fortunately, a seminal event occurred. Professor Mark Aizerman of the USSR gave a seminar at Berkeley where, amongst other things, he said that he had started to write a book on Control Theory but gave up the project because he did not think there was enough substance to it. Indeed the emperor had no clothes. (It is worth noting in the context of this lecture that eventually Aizerman moved to Pattern Recognition.)

Because I could not afford to abandon Control Theory without serious consequences I searched for a compromise, an area where applications would be acceptable. The field of Control Theory for Biological Models filled that role. It let me get away from pure mathematics(?) but still kept me within the confines of academia. I took some courses in Neurophysiology and had discussions with biologists, especially Professors Walter Freeman and the late Don Wilson. The ultimate results was a Ph.D. thesis with the title: Analysis and Synthesis of Pulse Frequency Modulation Feedback Systems (1964). The topic had been motivated by efforts to model neuronal transmission of information.

Part of that work lead me to the study of biological neural nets. I published a paper titled “A New Model for Simple Neural Nets and Its Application in the Design of a Neural Oscillator,” in the Bulletin of Mathematical Biophysics, 1965. There I tried to model the neuronal circuit controlling the flight of the locust. The model was using a mixture of difference and differential equations but no partial differential equations (as required by the Hodgkin-Huxley model). Hence the word “simple.”

Unfortunately, this happy state of affairs did not last long. A seminar given by Professor Jerry Letvin of M.I.T. at Berkeley was another seminal event. After the seminar he had individual discussions with graduate students and I took the opportunity to describe to him my research. He gave me two important pieces of advice: (a) My models had nothing to do with the nervous system (although they might be interesting systems in their own right); (b) However I should continue insisting in public that they were, otherwise I might lose my funding.

Letvin’s suggestions were re-enforced by another visitor, the late Leon Harmon of Bell Labs. He had constructed a circuit consisting of three "neurons" and was asking the audience to determine its structure by observing its response. It was a hopeless task.

Thus modeling of biological systems without a deep understanding of biology was not going to lead anywhere. I had reached another dead end, unless I wanted to become a biologist.

The solution to my dilemma came from another visitor at Berkeley. In the Spring of 1964 Nils Nilsson (then at SRI) gave a special topics course at Berkeley on "Learning Machines," essentially Statistical Pattern Recognition. That seemed to offer the right mixture of theory and applications and I realized that I had found my calling. However, given the academic realities I could not jump right in, so several years of “transition” followed as marked by the following dates: (a) My last control theory paper was published in 1967; (b) My last major biological modeling paper was published in 1975 (and a book in 1973); (c) My first pattern recognition paper was published in 1968. What these dates indicate is that by 1966 I had dropped control theory completely and I had started serious work in pattern recognition. Work in biological modeling continued in parallel with pattern recognition for about eight years.

2. The Early Years of Pattern Recognition (1965-1975)

When I entered the field, Statistical Pattern Recognition was the dominant approach. It was essentially an application of non parametric statistics. However, it suffered from a serious problem. Given that some separating hyper-surfaces have been determined from a training set, we could not say much about a solution to the problem without knowing the probability that new samples could be classified correctly. In other words, successful performance on a testing set is not a guarantee for future results unless we know that the present data are representative of everything likely to be encountered in the future. The only way to deal with this problem is to have information-preserving features, i.e. features that allow to reconstruct the original object from them. If this is impossible, we must have control over the loss of information (for example Fourier approximation). Of course, this is easier said than done.

 In the late 1960's and early 1970's it was becoming apparent that statistical pattern recognition should not be pushed too hard. The literature contained discussions on various related issues, such as over-training (Kanal) and the need to keep the degrees of freedom low (Duda and Hart). A more basic limitation (also discussed in Duda and Hart) was that choosing the optimal separating hyper-surface is important only if the misclassification error is high (a poor system). It is much less so if the misclassification error is low (a good system). This is illustrated in Figure 1.

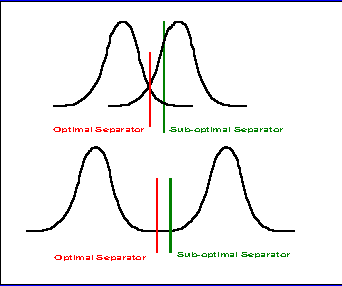
Figure 1: When the Classifier is Important. In the top example choosing the optimal classifier is important, but it is much less so in the bottom example.

It had become clear to several researchers that features were everything. In order to solve a pattern recognition problem  we need features that are: (a) information preserving (or the loss of information is controlled); (b) the resulting vectors cluster tightly within class and are far apart for different classes. If we can find such features and have a sufficient number of representative samples, then we are almost done! For such features a good classifier will complete the solution; otherwise no classifier will help.

Therefore the key task is to find good features. Several ideas were explored. One of the most obvious candidates was summations by series. Let X be the independent variable space (plane for images) and Y the signal space (scalar for monochrome images). For an appropriate function family (Fourier basis, moments, etc) we can express a signal as a summation of members of such a function family.

y(x) = Σ f_i F_i(x)  x in X,  y in Y

However such a representation may neither allow for controlled loss of information nor produce clustered feature vectors. Figure 2 illustrates this problem.

Figure 2: The Challenge of Matching Human Perception. Which of these three shapes is most different from the other two?

Most human observers will identify the middle shape as being the odd one. (The eccentricity of the ellipse on the right is hardly visible.) However the popular L₂ norm will single out the ellipse as the odd shape, contrary to human intuition. An L_inf norm or a Sobolev norm might or might not give the intuitive answer. On the other hand a polygonal (or a more general spline) approximation will produce the “right” answer.

2.1. Structural Pattern Recognition

The realization of the limitations of summations by series was the first step towards Structural Pattern Recognition. In particular, two questions arose. If sums are not good forms of representation why not try splines? But why stop there and not try labeled graphs? The key idea is to represent y(x) as a collection of “simpler” signals e_i(x) with the property that each one is zero over large parts of X. In other words, the focus should be on the structure of the signal. The concept of Structural Pattern Recognition was put forth in a paper in 1971 [1].

The desirability of understanding the structure of the problem is illustrated by the example of Figure 3.

Figure 3: What is the best mathematical tool to describe the difference between these two pictures? Direct comparison of pixel values will not provide the desired result.

Pet owners may find use for a Pet Monitor. When a pet goes to a place it is not supposed to be, a alarm sounds to warn the owner or to deter unwanted activity by the pet. The availability of inexpensive digital cameras makes such a project attractive.

It is clear that it will be very difficult to train a statistical classifier on a representative enough sample of pictures with dogs and surroundings. However, the problem becomes tractable if we understand its nature, identifying the presence of new objects in a scene. This can be achieved if we apply image segmentation to identify objects and then compare images taken at different times for the presence of new objects.

Note that direct image comparison may not work because of changing illumination conditions (recall the ellipse and the notched circle example).

2.2. Syntactic Pattern Recognition

Syntactic Pattern Recognition actually predates Structural Pattern Recognition (publications in the middle 1960’s). It also describes the input to the pattern recognition system as an aggregate of parts, but it places major emphasis on the rules of composition.

The approach is attractive because of well developed theory of formal languages. However, in spite of several theoretically appealing features and significant contributions by K.S. Fu, H. Bunke, A. Sanfeliu, and others, syntactic pattern recognition found only limited applications. This is due to two major negative factors: (1) The difficulty of Grammatical Inference. Not good algorithms have ever been found, but it has been shown that several formulations of the problem belong to the class of NP complete problems. (2) Syntactic rules are not always a good model on how the parts are joined to form the whole. The strength of the syntactical methods in the field of computer science relies on its suitability for dealing with recursion. However recursion is rarely present in pattern recognition applications.

3. Pattern Recognition in the Present (1980-2000)

3.1. Structural Pattern Recognition

Structural pattern recognition relies on  Segmentation (of Images, Curves, etc) and the extraction “interesting” relationships (possibly syntactic) between the parts found during segmentation. Features are defined either as properties of parts or as properties of relationships between parts. They may also be of syntactic nature, namely if a particular syntactic relation holds between certain parts, the value of a boolean feature may be set to one. The features found in this way may be used as input to a statistical classifier.

It is interesting to note a critique of the approach (May 1981): “Structural Pattern Recognition … lacks a sound theoretical basis … (instead one is supposed) to investigate the process by which pictorial data can be transformed into more tractable mathematical representations …” Indeed, Structural Pattern Recognition has no theoretical basis: it is based on the common sense observation that problems must be first understood before they can be solved. Structural Pattern Recognition is a philosophy rather than a methodology. It emphasizes the need to understand the nature of the problem and the desirability of models. It does not provide any systematic analytical framework the way Statistical and Syntactic Pattern Recognition do. If we consider pattern recognition an engineering problem, it is not surprising that no general methodologies are available.

3.2. A case study: OCR

An unstructured approach to Optical Character Recognition (OCR) consists of the following steps: (1) Conversion of the scanned document into a binary image; (2) Isolation of the individual characters; (3) Training of a statistical classifier (possibly a neural network) using a “large” number of samples. Note that if each sample is a 16 by 16 matrix, we have 2²⁵⁶ possible patterns, therefore “large” should be a nontrivial fraction of that number (at 1% we need about 2²⁵⁰ samples). There is no way to confirm theoretically that the resulting classifier is valid.

The structured approach to the same problem relies on an the investigation of models for character shape specification. Often such models are based on strokes, but they may also rely on contour concavities (S.Mori, K.Yamamoto), junctions or irregular parts (J.C.Simon), etc. Models of distortions and noise are also essential (H.S.Baird) and as a result we may compute features that describe the shape and are robust with respect to distortions and noise. The investigation of the shape and the rules of writing/printing/scanning provide additional suggestions for useful strategies, for example correction of tilt during pre-processing (H.S.Baird) It is easier to use statistical techniques since we need estimate a limited number of parameters. As long as our models capture the shape variations and noise effects we do not need an excessive number of samples.

3.3. Modern Statistical Techniques

The last decade has seen numerous papers on Neural Networks and Hidden Marcov models. While it has been proven (A.K. Jain) that  Neural Networks are equivalent to statistical classifiers, the new methodology may have some merit because it may provide more effective computational schemes. Hidden Marcov Models are doubly stochastic processes that have been explored mainly for speech recognition. The underlying Marcov process may correspond to changes in the shape of the vocal track. Observed sound corresponds to that shape.

3.4. The Reality of Bar Codes (Including Two-Dimensional Symbologies)

Today the use of bar codes is widespread and it is worthwhile to discuss why they are so much easier to read than printed text. The simplicity of reading is not only limited to the simple linear bar codes that we see every day in the food stores, but also extends to the two-dimensional symbologies such as shown in Figure 4. The following are some of the reasons for this property: (1) Bar codes (and two-dimensional symbologies) are designed to be read by machines, although they are unreadable by people (2) They have a well defined mathematical structure, therefore it is trivial to specify features; (3) Distortions and noise have been studied carefully and they are counteracted by the use of error detecting and error correcting codes; (4) Decoders (classifiers) are designed on the basis of the mathematical model rather than by training.

It should be pointed out that decoder specifications require no more than 10^-3 rejection rate and no more than 10^-6 symbol substitution rate (“misdecode”). It is impractical to confirm such rates by actual scanning, therefore large scale simulation tests are used to confirm that parameter selection results in error rates that meet the specifications. There is a lesson for OCR here: Carefully designed simulations might be better than “real” tests.

Figure 4: Examples of two-dimensional symbologies. Maxicode is used by United Parcel Service for tracking packages, while PDF417 has found numerous uses in securing official documents, etc.

4. Suggestions for the Future

I would like to offer several suggestions for succeeding in pattern recognition research.

(1) It is important to keep a focus on Engineering. Pattern Recognition is Engineering because we try to design machines that read documents, count blood cells, inspect parts, etc. We must understand the “physics” of the problem and select from amongst available tools the ones appropriate for the problem. It is futile to look for general mathematical/computational techniques that can solve all problems. In spite of numerous claims over the last half century, none has been found.

(2) We must be brave and be ready to discard old problem formulations. While the recognition of hand-writing remains an open problem, users of modern palmtops can provide handwritten input to computers. This is achieved by imposing constraints on the shape of letters and the order of writing. An example of the system is shown in Figure 5.

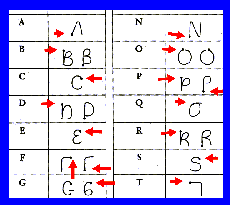
Figure 5: Example of Graffiti, invented by David Goldberg at Xerox PARC [2]. Red arrows mark the start of each character.

(3) We must be aware of the Complexity of the Human Brain. The model of simple units connected to all others is false. The brain is highly structured; true each neuron is connected to thousands of others, but there are billions of them. Also human actions are not the result of logical decision processes. It seems that emotion is essential for decision making! See Damasio’s book: Descartes’ Error [3].

(4) We must be aware of the Complexity of Human Vision. S. Zeki suggests four visual systems, each with distinct perceptual function: motion, color, and shape (two systems). One of the shape systems acts also as an integrator [4]. In a more recent work V. S. Ramachandran [5] mentions 30 different areas in the brain that are responsible for visual processing. There is evidence from research in both neurophysiology and cognitive psychology that human vision is top down as well as bottom up.

(5) We must remember the Turing/Wiener Story. A. Hodges in his biography of Alan Turing [6] describes a meeting between Turing and Norbert Wiener. Turing had started research on OCR as well as other computational problems. Wiener told him not to waste his time because all such problems had been solved by the Neural Nets invented by McCulloch and Pitts at MIT. Turing is reported to have used an unkind term for McCulloch. 55 years later most of these problems are still open.

A corollary of the complexity of human vision is that we should avoid naďve computational models that purport to model human vision. Pattern recognition should be approached as a complex signal transformation problem.

(6) We should keep in mind the importance of Error Detection and Error Correction. All modern communication systems use error detection, and frequently, error correction as well. How can we implement this approach in pattern recognition? Dual (or multiple) processing of input by different methods and comparison of results offers the advantages of error detection and error correction. The multiclassifier approach (Srihari, T.K.Ho) follows this philosophy, but there is room for more work.

(7) We need to recognize the importance of “Middle Vision”. Researchers should choose problems carefully by moving away from low level vision into a level where large structures can be identified. For example: Edge detection has been solved a long time ago. Object outlining is still an open problem. Thinning (esp. pixel based) and curve fitting have been worked to death. We need methods to identify strokes (S.Mori and Suzuki).

(8) Before attempting low level recognition we may attempt to recognize the context or environment. In OCR this would be recognition of font (advocated for a long time by G. Nagy), line tilt, etc. In the case of “natural” scenes would be direction and intensity of illumination, etc. Recognition of details is going to be easier once we have the “big picture” right. Examples of practical successes with the help of context recognition include the improved recognition of postal addresses using the database of streets and ZIP codes (J.Hull et al, CEDAR at SUNY Buffalo) and the American Express amount verification: number in check is read and compared to (the known) amount owed (Frank Mullin at TRW). Unfortunately, it is difficult to find examples in the literature since such work violates the rules of the Glassperlenspiel. For example, papers on 2D barcodes never made past the IEEE Transactions review process.

(9) Apply the lessons learned from Chess Machines. Thus, the The designers of the IBM chess playing machines describe their creation as a means for enhancing the chess playing ability of an individual. A key team member was a chess grandmaster. In effect he beat the world champion with the help of the computer.

(10) Look for New Areas. Amongst the promising areas where pattern recognition can be applied is are e-commerce and User Interfaces. In e-commerce the term Data Mining is just another word for Pattern Recognition, where the patterns are searched over database records. Not surprisingly, feature selection appears to be the key issue rather than classification techniques. See the book by Berry and Linoff [7]. User interfaces can be improved by applying Pattern Recognition to the input provided by the user. Microsoft Word and several other software tools in the market offer limited use of the concept.

In short: The prospects are Bright if we approach pattern recognition as an engineering problem and try to solve important special cases while staying away from the Glassperlenspiel. The prospects are Grim if we keep looking for silver bullets that will solve “wholesale” a large range of general problems, especially if we harbor the illusion of doing things the way the human brain does.

Acknowledgements and Excuses

I want to thank Henry Baird for arranging a "dry run" of the lecture at Xerox PARC in June of 2000. Henry's comments and those of David Goldberg, David Fleet, and other members of the audience were very helpful in revising the lecture.

I also want to thank the National Science for the support of my research for close to 30 years by a program first headed by Norman Caplan and then by Howard Moraff. I am particularly grateful that the support came through without strings attached to it and was made available even when what I did was out of fashion.

Over the years my laboratory also received support from several mission oriented agencies and industry. In rough chronological order these include the U.S. Army Research Office, the U.S. Postal Service, Lockheed Aerospace, Grumman Data Systems, Ricoh Ltd of Japan, Sony of Japan, and Symbol Technologies.

This text version of the lecture is long overdue. A few weeks after returning home from ICPR 2000 I was hospitalized and underwent open heart surgery with the result that my writing plans were completely upset. In the text I am referring to the contributions of several people without citing any specific works. I am afraid that time constraints do not allow me to complete that task.

A slightly edited version of this document has been published in Pattern Recognition Letters, vol. 24 (Jan. 2003), pp. 1-7.

Literature cited

1. T. Pavlidis “Structural Pattern Recognition: Primitives and Juxtaposition Relations,” in Frontiers of Pattern Recognition, M. S. Watanabe, ed., 1972.
2. D. Goldberg and C. Richardson “Touch-Typing with a Stylus,” Proc. INTERCHI’93, Amsterdam, April 1993, pp. 80-87.
3. A. R. Damasio Descartes’ Error: Emotion, Reason, and the Human Brain, Avon Books, New York, 1994.
4. .S. Zeki “The Visual Image in Mind and Brain,” Scientific American, vol. 267, No. 3 (Sept. 1992), pp. 69-76.
5. V.S. Ramachandran and S. Blakeslee Phantoms in the Brain, William Morrow and Company Inc., New York, 1998.
6. A. Hodges Alan Turing:the Enigma, Touchstone, 1983, pp. 404, 411.
7. M.J.A. Berry and G, Linoff Mastering Data Mining, Wiley, 2000.